সপ্তম শ্রেণির গণিত পাঠ্যবইয়ের প্রথম, নবম ও দশম অধ্যায়ের সাথে সম্পর্কিত কিছু অতিরিক্ত বিষয়বস্তু সংযুক্তি হিসেবে যুক্ত করা হয়েছে। কারণ ২০২৫ সালে সপ্তম শ্রেণিতে অধ্যয়নরত শিক্ষার্থীরা পূর্বতন শ্রেণিতে (ষষ্ঠ শ্রেণি) 'জাতীয় শিক্ষাক্রম ২০২২' অনুযায়ী অধ্যয়ন করেছে। 'জাতীয় শিক্ষাক্রম ২০২২' অনুযায়ী ষষ্ঠ শ্রেণির গণিত পাঠ্যপুস্তকে উক্ত বিষয়বস্তু অন্তর্ভুক্ত ছিল না। তাই শিখনের ধারাবাহিকতা ও কার্যকর শিখনের জন্য উক্ত বিষয়বস্তু সংযুক্ত করা হয়েছে।
উল্লেখ্য যে, সপ্তম শ্রেণির গণিত বিষয়ের শিখনফল অনুযায়ী ধারাবাহিক ও সামষ্টিক মূল্যায়ন অনুষ্ঠিত হবে।
আমরা আগের শ্রেণিতে জেনেছি, যে চতুর্ভুজের চারটি বাহু সমান এবং প্রতিটি কোণ সমকোণ তাকে বর্গ বলা হয় (চিত্র-১.১.১)। আর বর্গের বাহুর দৈর্ঘ্য এ একক হলে বর্গক্ষেত্রের ক্ষেত্রফল a2 বা (a a) বর্গ একক হবে। বিপরীতভাবে বলা যায়, বর্গক্ষেত্রের ক্ষেত্রফল a2 বা (aa) হলে এর প্রতিটি বাহুর দৈর্ঘ্য a একক হবে।
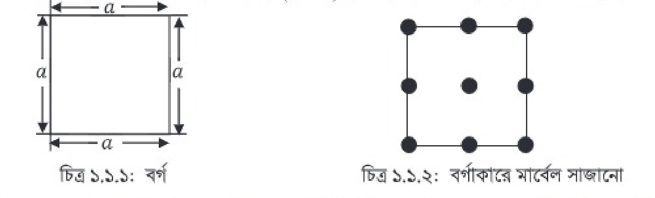
উপরের চিত্র ১.১.২ থেকে দেখা যাচ্ছে, সমান দূরত্বে প্রতিটি সারিতে ৩টি করে এবং ৩টি সারিতে মার্বেল সাজানো হয়েছে। তাই মোট মার্বেলের সংখ্যা () = ৩২ = ৯টি। এখানে প্রতিটি সারিতে মার্বেলের সংখ্যা ৩টি এবং সারির সংখ্যাও ৩টি। তাই মার্বেল সাজানোর চিত্রটি বর্গাকার হয়েছে। সুতরাং ৩ এর বর্গ ৯ এবং ৯ এর বর্গমূল ৩।
| উপরের আলোচনা থেকে বলা যায়, কোনো সংখ্যাকে সেই সংখ্যা দ্বারা গুণ করলে যে গুণফল পাওয়া যায় তা ঐ সংখ্যার বর্গ এবং সংখ্যাটি হলো ঐ গুণফলের বর্গমূল। যেমন: () = ২২ = 8 এখানে ২ এর বর্গ হলো ৪ এবং ৪ এর বর্গমূল হলো ২। |
আমরা আগের শ্রেণিতে জেনেছি, স্বাভাবিক সংখ্যা, শূন্য ও ঋণাত্মক সংখ্যা একত্রে মিলে পূর্ণসংখ্যা হয়। তাই নিচের সারণিতে কিছু পূর্ণসংখ্যা দেওয়া আছে, তাদের বর্গ নির্ণয় করো।

উপরের সারণি থেকে দেখা যাচ্ছে, কিছু কিছু স্বাভাবিক সংখ্যা যেমন: ১, ৪, ৯, ১৬, ২৫, ৩৬, ৪৯, ……….. ইত্যাদি এদের বৈশিষ্ট্য এমন যে, এ সংখ্যাগুলোকে অন্যকোনো পূর্ণসংখ্যার বর্গ হিসেবে প্রকাশ করা যায়। তাই এদেরকে পূর্ণবর্গ সংখ্যা বলা হয়। সারণি থেকে স্পষ্টত দেখা যাচ্ছে যে, সকল পূর্ণসংখ্যার বর্গ একটি স্বাভাবিক সংখ্যা। আর এই স্বাভাবিক পূর্ণবর্গ সংখ্যাগুলোর বর্গমূল একটি পূর্ণসংখ্যা। যেমন: ৯ একটি পূর্ণবর্গ সংখ্যা এবং এটা একটি স্বাভাবিক সংখ্যা। কিন্তু এর বর্গমূল হলো ৩ ও-৩, যা একটি পূর্ণসংখ্যা।
| উপরের আলোচনা থেকে বলা যায়, কোনো একটি স্বাভাবিক সংখ্যা m কে যদি অন্য একটি পূর্ণসংখ্যা n এর বর্গ (n²) আকারে প্রকাশ করা যায়, তাহলে m কে n এর বর্গ সংখ্যা বলা হয় এবং n কে m এর বর্গমূল বলা হয়। |
নিচের সারণিতে ১ থেকে ২০ পর্যন্ত সংখ্যার বর্গ সংখ্যা দেওয়া হয়েছে। খালি ঘরগুলো পূরণ কর।


উপরের সারণিভুক্ত পূর্ণবর্গ সংখ্যাগুলো থেকে দেখা যাচ্ছে যে, পূর্ণবর্গ সংখ্যাগুলোর একক স্থানীয় অঙ্ক ০, ১, ৪, ৫, ৬ ও ৯। কিন্তু কোনো পূর্ণবর্গ সংখ্যার একক স্থানীয় অঙ্ক ২, ৩, ৭ ও ৮ নেই।
| কাজ: ১। কোনো সংখ্যার একক স্থানীয় অঙ্ক ০, ১, ৪, ৫, ৬ ও ৯ হলেই কি সংখ্যাটি পূর্ণবর্গ সংখ্যা হবে? ২। নিচের সংখ্যাগুলোর কোনগুলো পূর্ণবর্গ সংখ্যা নির্ণয় কর। ২০৬২, ১০৫৭, ২৩৪৫৩, ৩৩৩৩৩, ২৫০০, ৫২৯, ৩০০, ১০৬৮ ৩। পাঁচটি সংখ্যা লিখ, যার একক স্থানীয় অঙ্ক দেখেই তা পূর্ণবর্গ সংখ্যা নয় সিদ্ধান্ত নেওয়া যায়। |
এবার সারণি থেকে একক স্থানে ১ রয়েছে এমন বর্গসংখ্যা নিই।

উপরের আলোচনা থেকে নিচের সিদ্ধান্ত নেওয়া যায়-
১। যে সব সংখ্যার সর্ব ডানদিকের অঙ্ক অর্থাৎ একক স্থানীয় অঙ্ক যদি ২ বা ৩ বা ৭ বা ৮ হয়, তাহলে সেই সংখ্যাটি পূর্ণবর্গ সংখ্যা নয়।
২। যে সব সংখ্যার সর্ব ডানদিকের অঙ্ক অর্থাৎ একক স্থানীয় অঙ্ক যদি ০ বা ১ বা ৪ বা ৫ বা ৬ বা ৯ হয়, তাহলে সেই সংখ্যাটি পূর্ণবর্গ সংখ্যা হতে পারে। যেমন: ১, ৮১, ৬৪, ২৫, ৩৬, ৪৯, .. ইত্যাদি। আবার নাও হতে পারে। যেমন: ১১, ৮৬, ৯০, ৩৫, ৭৪, ১৯৯, ... ইত্যাদি।
৩। যে সব সংখ্যার ডানদিক থেকে বিজোড় সংখ্যক শূন্য থাকে, সেই সংখ্যাটি পূর্ণবর্গ সংখ্যা হতে পারে না।
যেমন: ৯০, ৩০০০, ৪০০০০০, ………….. ইত্যাদি।
৪। যে সব সংখ্যার ডানদিক থেকে জোড় সংখ্যক শূন্য থাকে, সেই সংখ্যাটি পূর্ণবর্গ সংখ্যা হতে পারে। যেমন: ১০০, ৪০০, ২৫০০, ……….. ইত্যাদি। আবার নাও হতে পারে। যেমন: ১৩০০, ৩০০, ৫০০, ……. ইত্যাদি।
কাজ: ১। সারণি থেকে পূর্ণবর্গ সংখ্যার একক স্থানীয় অঙ্কে ৪ রয়েছে, এরূপ সংখ্যার জন্য নিয়ম তৈরি কর। ২। নিচের সংখ্যাগুলোর মধ্যে থেকে পূর্ণবর্গ সংখ্যাটির একক স্থানীয় অঙ্কটি কত হবে? |
উদাহরণ ৬। ৯৭২ এর সাথে কোন ক্ষুদ্রতম সংখ্যা গুণ করলে গুণফল একটি পূর্ণবর্গ সংখ্যা হবে?
সমাধান: প্রথমেই ৯৭২ সংখ্যাটির মৌলিক উৎপাদক বিশ্লেষণ করি।

মৌলিক উৎপাদক বিশ্লেষণ করে পাই, ৯৭২ = (২ ২) (৩ ৩) (৩ ৩) ৩
এখন ৯৭২ এর মৌলিক উৎপাদক বিশ্লেষণ থেকে দেখা যাচ্ছে, ২ উৎপাদকটি দুইবার আর ৩ উৎপাদকটি পাঁচবার আছে অর্থাৎ ৩ উৎপাদকটি বিজোড় সংখ্যক আছে। আমরা জানি, পূর্ণবর্গ সংখ্যার মৌলিক উৎপাদকগুলো জোড়ায় জোড়ায় থাকে। তাই ৩ উৎপাদকটির জোড়া করতে হবে। এ জন্য ৯৭২ কে ৩ দ্বারা গুণ করলে গুণফলটি একটি পূর্ণবর্গ সংখ্যা হবে।
সুতরাং নির্ণেয় ক্ষুদ্রতম সংখ্যা = ৩
উদাহরণ ৭। ১৫৬৮ এর সাথে কোন ক্ষুদ্রতম সংখ্যা ভাগ করলে গুণফল একটি পূর্ণবর্গ সংখ্যা হবে?
সমাধান: প্রথমেই ১৫৬৮ সংখ্যাটির মৌলিক উৎপাদক বিশ্লেষণ করি।

মৌলিক উৎপাদক বিশ্লেষণ করে পাই, ১৫৬৮ = (২ ২) (২২) ২ (৭ ৭)
এখন ১৫৬৮ এর মৌলিক উৎপাদক বিশ্লেষণ থেকে দেখা যাচ্ছে, ২ উৎপাদকটি পাঁচবার আর ৭ উৎপাদকটি
দুইবার আছে অর্থাৎ ২ উৎপাদকটি বিজোড় সংখ্যক আছে। আমরা জানি, পূর্ণবর্গ সংখ্যার মৌলিক উৎপাদকগুলো জোড়ায় জোড়ায় থাকে। তাই ২ উৎপাদকটির জোড়া করতে হবে। সুতরাং ১৫৬৮ কে ২ দ্বারা ভাগ করলে ভাগফলটি একটি পূর্ণবর্গ সংখ্যা হবে।
সুতরাং নির্ণেয় ক্ষুদ্রতম সংখ্যা = ২
আমরা আগের শ্রেণিতে জেনেছি, তিনটি সরলরেখাংশ দ্বারা আবদ্ধ চিত্রকে ত্রিভুজ বলে [চিত্র ১]।

১. চিত্র ১ থেকে দেখা যাচ্ছে, AB, BC ও AC এই তিনটি সরলরেখাংশ দিয়ে একটি ত্রিভুজ ABC গঠিত হয়েছে। তাই AB, BC ও AC এই প্রত্যেকটি রেখাংশই ত্রিভুজ ABC এর বাহু (side)।
| যে তিনটি সরলরেখাংশ দিয়ে ত্রিভুজ গঠিত হয় তাদের প্রত্যেকটিকে ঐ ত্রিভুজের বাহু (side) বলা হয়। |
২. চিত্রে দেখা যাচ্ছে, AB ও AC বাহু দুইটি পরস্পর A বিন্দুতে; AB ও BC বাহু দুটি পরস্পর B বিন্দুতে এবং AC ও BC বাহুদ্বয় পরস্পর C বিন্দুতে ছেদ করেছে। তাই A, B, C এই প্রতিটি বিন্দুকেই ∆ABC এর শীর্ষবিন্দু বলা হয়। ইংরেজি বড়ো হাতের অক্ষর ও শীর্ষবিন্দু দিয়ে ত্রিভুজের নামকরণ করা হয়। যেমন: চিত্রের ত্রিভুজের শীর্ষবিন্দুগুলো হলো A, B, C. তাই চিত্রের ত্রিভুজের নামকরণ ∆ABC করা হয়েছে।
| যেকোনো ত্রিভুজের দুটি বাহু পরস্পর যে বিন্দুতে ছেদ করে সেই বিন্দুকে ঐ ত্রিভুজের শীর্ষবিন্দু (vertex) বলা হয়। ত্রিভুজের শীর্ষবিন্দুর নামানুসারে ত্রিভুজের নামকরণ করা হয়। |
৩. চিত্রে দেখা যাচ্ছে, A, B ও C শীর্ষবিন্দু তিনটিতে যথাক্রমে ∠BAC, ∠ABC ও ∠ACB উৎপন্ন করেছে। এই প্রত্যেকটি কোণকে ∆ABC এর শীর্ষকোণ (vertical angle) বলা হয়। কখনো কখনো এটিকে শিরঃকোণও বলা হয়। যেহেতু যেকোনো ত্রিভুজের শীর্ষবিন্দু তিনটি তাই প্রত্যেকটি ত্রিভুজের তিনটি শীর্ষবিন্দু উৎপন্ন হয়।
| যেকোনো ত্রিভুজের শীর্ষবিন্দুতে যে কোণ উৎপন্ন হয়, তাকে ঐ ত্রিভুজের শীর্ষকোণ বলা হয়। যেহেতু যেকোনো ত্রিভুজের শীর্ষবিন্দু তিনটি তাই প্রত্যেকটি ত্রিভুজের তিনটি শীর্ষকোণ উৎপন্ন হয়। |
মনে করি, ABC যেকোনো একটি ত্রিভুজ, যার A, B ও C তিনটি শীর্ষবিন্দুতে উৎপন্ন কোণগুলো যথাক্রমে ∠BAC, ∠ABC ও ∠ACB এবং বাহু তিনটি হলো AB, BC ও AC।
এখন ∆ABC এর তিনটি বাহু AB, BC ও AC এর মধ্য বিন্দুগুলো যথাক্রমে D, E ও F নির্ণয় করি [চিত্র ২] এবং প্রতিটি বাহুর মধ্য বিন্দু ও তার বিপরীত শীর্ষবিন্দু সংযোগ করি। এতে ∆ABC এ AD, BE ও CF এই তিনটি সরলরেখাংশ পাওয়া যাচ্ছে। AD, BE ও CF এই তিনটি রেখাংশের প্রত্যেকটিকে ∆ABC এর মধ্যমা বলা হয়।
| যেকোনো ত্রিভুজের যেকোনো শীর্ষবিন্দু থেকে তার বিপরীত বাহুর মধ্যবিন্দুর সংযোগ সরলরেখাংশকে ঐ ত্রিভুজের মধ্যমা বলা হয়। |
মনে করি, ABC যেকোনো একটি ত্রিভুজ, যার A. B ও C তিনটি শীর্ষবিন্দু এবং তার তিনটি বাহ AB. BC ও AC। এখন ∆ABC এর তিনটি শীর্ষবিন্দু A, B ও C থেকে তার বিপরীত বাহুর উপর বা বর্ধিতাংশের উপর লম্ব আঁকি
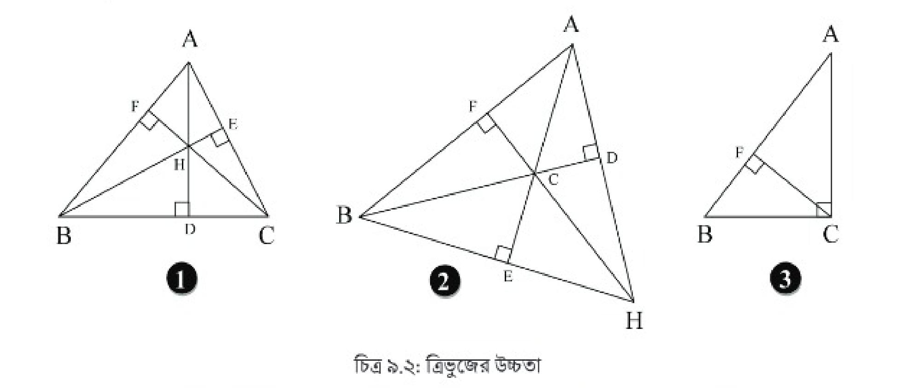
১. চিত্র ৯.২ (1) থেকে দেখা যাচ্ছে যে, ∆ABC এর তিনটি শীর্ষবিন্দু A, B, C হতে তাদের বিপরীত বাহু যথাক্রমে BC, AC, AB এর উপর AD, BE, CF লম্ব আঁকা সম্ভব হয়েছে।
২. চিত্র ৯.২ (2) থেকে দেখা যাচ্ছে যে, ∆ABC এর শীর্ষবিন্দু C হতে এর বিপরীত বাহু AB এর উপর CF লম্ব আঁকা সম্ভব হয়েছে। কিন্তু শীর্ষবিন্দু A ও B হতে তাদের বিপরীত বাহু যথাক্রমে BC, AC এর উপর AD, BE লম্ব আঁকা সম্ভব হয়নি। তবে BC ও AC বাহুর বর্ধিতাংশের উপর AD, BE লম্ব আঁকা সম্ভব হয়েছে।
৩. চিত্র ৯.২ (3) থেকে দেখা যাচ্ছে যে, ∆ABC এর তিনটি শীর্ষবিন্দু A, B, C হতে তাদের বিপরীত বাহ যথাক্রমে BC, AC ও AB এর উপর AD, BE ও CF লম্ব আঁকা সম্ভব হয়েছে। তবে A ও B থেকে তার বিপরীত বাহু যথাক্রমে BC ও AC এর উপর AC ও BC নিজেরাই লম্ব।
একটি ত্রিভুজের তিনটি শীর্ষবিন্দু থাকে। তাই শীর্ষবিন্দুগুলো থেকে বিপরীত বাহুর উপর বা তার বর্ধিতাংশের উপর তিনটি লম্ব আঁকা যায়। এই প্রত্যেকটি লম্বকেই ABC ত্রিভুজের উচ্চতা বলা যায়। তবে যে বাহকে ভূমি বিবেচনা করা হয় সেই বাহুর বা বাহুর বর্ধিতাংশের উপরের লম্বকেই ঐ ত্রিভুজের উচ্চতা বিবেচনা করা হয়।
| যেকোনো ত্রিভুজের ভূমির বিপরীত শীর্ষবিন্দু হতে ভূমির উপর বা ভূমির বর্ধিতাংশের উপর অঙ্কিত লম্বকে ঐ ত্রিভুজের উচ্চতা বলা হয়। আর কোনো ত্রিভুজের যে বিন্দুতে উচ্চতা বা তার বর্ধিতাংশ তিনটি পরস্পরকে ছেদ করে সেই বিন্দুকে লম্ববিন্দু বলা হয়। |
ধরি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি বাহু AB, BC ও AC।

উপরের চিত্রের ∆ABC এর ভিতরের দিকে তিনটি শীর্ষবিন্দুতে ∠BAC, ∠ABC ও ∠ACB উৎপন্ন করেছে। এই কোণ তিনটিকে ত্রিভুজের অন্তঃস্থকোণ বলা হয়।
| যেকোনো ত্রিভুজের তিনটি শীর্ষবিন্দুতে ত্রিভুজের ভিতরের দিকে যে তিনটি কোণ উৎপন্ন হয় তাদেরকে ত্রিভুজের অন্তঃস্থকোণ বলা হয়। |
মনে করি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি বাহ AB, BC ও AC এবং তিনটি কোণ ∠ABC, ∠ACB ও ∠BAC। এখন ∆ABC এর যেকোনো একটি বাহু BC কে D পর্যন্ত বর্ধিত করি । এতে ∆ABC এর বাইরের দিকে ∠ACD উৎপন্ন হয়েছে। এই কোণকে কী কোণ বলব?

∆ABC এর ∠ABC, ∠ACB ও ∠BAC কে অন্তঃস্থ কোণ বলা হয়। আর ∠ACD কে বহিঃস্থ কোণ বলা হয়।
| যেকোনো ত্রিভুজের যেকোনো বাহকে যেকোনো দিকে বর্ধিত করলে বাইরের দিকে যে কোণ উৎপন্ন হয় তাকে ঐ ত্রিভুজের বহিঃস্থ কোণ বলা হয়। |
উপরের চিত্রে দেখা যাচ্ছে, বহিঃস্থ ∠ACD এর সন্নিহিত কোণ হলো ∠ACB। কিন্তু ∠ABC ও ∠BAC কোণ দুটিকে কী কোণ বলব?
∆ABC এ, ∠ABC ও ∠BAC কোণ দুটিকে বহিঃস্থ ∠ACD এর অন্তঃস্থ বিপরীত কোণ বলা হয়।
| যেকোনো ত্রিভুজের বহিঃস্থ কোণের সন্নিহিত কোণ ছাড়া ত্রিভুজের অভ্যন্তরে যে দুটি কোণ থাকে তাদেরকে ঐ বহিঃস্থ কোণের অন্তঃস্থ বিপরীত কোণ বলা হয়। |
মনে করি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি কোণ ∠ABC, ∠ACB ও ∠BAC। এখানে △ABC এর তিনটি কোণের সমষ্টি অর্থাৎ (∠ABC+∠ACB + ∠BAC) নির্ণয় করতে হবে
অঙ্কন: A বিন্দু দিয়ে BC || PQ আঁকি।

চিত্র থেকে দেখা যাচ্ছে, BC || PQ এবং এদের ছেদক AB। তাই ছেদক বিপরীত পাশে উৎপন্ন ∠ABC ও ∠PAB একান্তর কোণ দুটি সমান। অর্থাৎ ∠ABC = ∠PAB = x ... (i)
আবারো দেখা যাচ্ছে, BC || PQ এবং এদের ছেদক AC। তাই ছেদকের বিপরীত পাশে উৎপন্ন ∠ACB ও ∠QAC একান্তর কোণ দুটি সমান। অর্থাৎ ∠ACB = ∠QAC = y ... (ii)
আবার PQ রেখার A বিন্দুতে AB রেখা ছেদ করায় ∠BAP ও ∠BAQ দুইটি সন্নিহিত কোণ উৎপন্ন করেছে। তাই আমরা লিখতে পারি:
∠BAP + ∠BAQ = 180°
∠BAP + ∠BAC + ∠CAQ = 180° [∠BAC + ∠CAQ = ∠BAQ]
ZABC+∠BAC + ∠ACB = 180°
অর্থাৎ ∆ABC এর তিনটি অন্তঃস্থ কোণের সমষ্টি 180° বা দুই সমকোণ।
| যেকোনো ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি 180° এবা দুই সমকোণ। এটা ইউক্লিডের প্রতিজ্ঞা ৩২। |
আমাদের চারদিকে বিভিন্ন আকৃতি (shape) ও আকার (size) এর বস্তু দেখতে পাই। তাই এই দুটি জিনিস নিয়ে পরিষ্কার ধারণা থাকা দরকার। তাই নিচের চিত্রগুলো ভালো করে দেখি।

১. চিত্র 1 ও 2 এর আকৃতি ভিন্ন ভিন্ন কিন্তু আকার একই। অর্থাৎ ছবি দুটি পরিমাপের দৃষ্টিতে সমান কিন্তু দেখতে আলাদা।
২. চিত্র 3 ও 4 এর আকৃতি একই কিন্তু আকার ভিন্ন ভিন্ন। অর্থাৎ ছবি দুটি দেখতে একই রকম কিন্তু পরিমাপের দৃষ্টিতে আলাদা। এই ধরনের জিনিসগুলোকে পরস্পরের সদৃশ বলা হয়।
৩. চিত্র 5 ও 6 এর আকৃতি ও আকার উভয়ই একই। অর্থাৎ ছবি দুটি দেখতে একই রকম এবং পরিমাণগত দিক থেকেও সমান। তাই এরা দেখতে হুবহু সমান। এই ধরনের জিনিসগুলোকে পরস্পরের সর্বসম বলা হয়।
এই অধ্যায়ে আমরা জ্যামিতির দুটি অত্যন্ত গুরুত্বপূর্ণ ধারণা- সর্বসমতা ও সদৃশতা নিয়ে আলোচনা করব। তবে আমরা শুধুমাত্র সমতলীয় সর্বসমতা ও সদৃশতা মধ্যেই আলোচনা সীমিত রাখব।
নিচের সমতলীয় চিত্রগুলো দেখে তাদের আকার ও আকৃতি নিয়ে আলোচনা করি।
১. পুরোপুরি ঢাকা হচ্ছে, কোনো ছোটো জিনিসকে তারচেয়ে বড় জিনিস দিয়ে ঢেকে দেওয়া। এখানে চিত্র ২-এ দেখা যাচ্ছে, ABCD তলের সম্পূর্ণ অংশকে EFGH তল দ্বারা ঢাকা হয়েছে। বিপরীতভাবে বলা যায় EFGH তলের কিছু অংশকে ABCD তল দ্বারা ঢাকা হয়েছে। তাই বলা যায়, এই দুটি চিত্র আকৃতিতে একই হলেও আকারে ভিন্ন ভিন্ন। একারণে ABCD ও EFGH সর্বসম নয়।
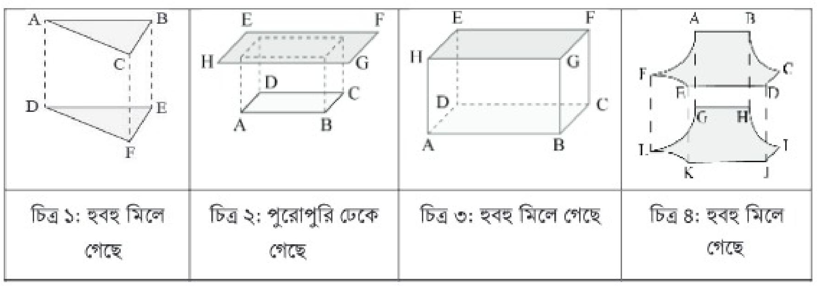
২. হবহু ঢাকা বা সর্বতোভাবে মিলার যাওয়ার অর্থ হচ্ছে, কোনো একটি জিনিসের প্রতিটি বিন্দুর সাথে অন্য একটি জিনিস মিলে যাওয়া। এখানে চিত্র ১, ৩, ৪ থেকে যথাক্রমে দেখা যাচ্ছে, ABC তলটি DEF দ্বারা, ABCD তলটি EFGH দ্বারা ও ABCDEF তলটি GHIJKL দ্বারা হুবহু ঢেকে বা সর্বতোভাবে মিলে গেছে। তাই এই চিত্রগুলোর আকৃতি ও আকার উভয়ই একই। একারণে এগুলো সর্বসম ও সর্বদা সমান।
৩. চিত্র ৩ থেকে দেখা যাচ্ছে, AB রেখাংশটি GH রেখাংশ দ্বারা হুবহু ঢেকে বা সর্বতোভাবে মিলে গেছে তাই AB ও GH পরস্পর সর্বসম। আবার চিত্র ২ থেকে দেখা যাচ্ছে, AB রেখাংশটি GH দ্বারা আংশিকভাবে ঢেকে গেছে AB ও GH পরস্পর সর্বসম নয় এবং দৈর্ঘ্যও অসমান। সুতরাং বলা যায়, দুটি রেখাংশের দৈর্ঘ্য সমান হলেই তারা পরস্পর সর্বসম হবে।
৪. চিত্র ৫ ও ৬ থেকে যথাক্রমে দেখা যাচ্ছে, ∠ABC = 40° ও ∠DEF = 40° তাই ∠ABC = ∠DEF অর্থাৎ কোণ দুটির মান সমান। দুটো কোণের মান সমান হলে তাদের পরস্পরকে হুবহু ঢাকা বা সর্বতোভাবে মিলে যায়। একারণে তারা পরস্পর সর্বসম ও সমান। আবার চিত্র ৬ ও ৭ থেকে যথাক্রমে দেখা যাচ্ছে, ∠DEF = 40° ∠RST = 60° অর্থাৎ কোণ দুটির মান অসমান। তাই দুটি কোণের মান অসমান হওয়ায় তারা পরস্পরকে হবহু ঢাকা বা সর্বতোভাবে মিলে যাচ্ছে না। এ কারণে তারা পরস্পর সর্বসম নয় ও তারা পরস্পর অসমান।

উপরের উদাহরণগুলো থেকে বলা যায়, একটি বস্তুর সাথে অপর একটি বস্তু দ্বারা হুবহু ঢাকা বা সর্বতোভাবে মিলে যায়, তাহলে ঐ বস্তু দুটিকে পরস্পরের সর্বসম বলা হয়।
| যখন একটি বস্তুর সাথে অপর একটি বস্তু দ্বারা হৰহ ঢাকা বা সর্বতোভাবে মিলে যায়, তখন ঐ বস্তু দুটিকে পরস্পরের সর্বসম বলা হয়। অন্যভাবে, যখন দুটি বস্তুর আকৃতি ও আকার উভয়ই একই রকম হয়, তখন সেই বস্তু দুটিকে সর্বসম বলা হয়। |
এখন যদি ABCD ও EFGH পরস্পর সর্বসম হয়, তহলে আমরা ABCD = EFGH এভাবে লিখে প্রকাশ করি। এর অর্থ হলো ABCD ও EFGH পরস্পর সর্বসম।
১. পরের পৃষ্ঠার চিত্র ১ থেকে দেখা যাচ্ছে, ∆ABC ও △DEF পরস্পরের সাথে হুবহু বা সর্বতোভাবে মিলে গেছে এবং দুটি ত্রিভুজের আকার ও আকৃতি উভয়ই একই রকমের হয়, তাই ত্রিভুজ দুটিকে সর্বসম বলা হয়।
অন্যভাবে বলা যায়, একটি ত্রিভুজ দিয়ে অন্য আরেকটি ত্রিভুজকে যদি হুবহু বা সর্বতোভাবে মিলে যায়, তাহলে ত্রিভুজ দুটিকে সর্বসম বলা হয়। এখানে হবহু বা সর্বতোভাবে মিলে যাওয়ার অর্থ হলো কোনো একটি ত্রিভুজের প্রতিটি বিন্দুর সাথে অন্য একটি ত্রিভুজের প্রতিটি বিন্দুর হুবহু বা সর্বতোভাবে মিলে যাওয়া বুঝায়। তাই দুটি ত্রিভুজ যদি সর্বসম হয়, তাহলে ঐ ত্রিভুজ দুটির অনুরূপ বাহুগুলো ও অনুরূপ কোণগুলো পরস্পর সমান হয়ে যায়।

১. উপরের চিত্র ২ থেকে দেখা যাচ্ছে, ∆ABC ও ∆DEF পরস্পরের সাথে হবহু বা সর্বতোভাবে মিলে যায়নি এবং দুটি ত্রিভুজের আকৃতি একই হলেও আকার ভিন্ন ভিন্ন ত্রিভুজ দুটি সর্বসম নয়।
| দুটি ত্রিভুজের যদি আকার ও আকৃতি উভয়ই একই রকমের হয়, তাহলে ত্রিভুজ দুটিকে সর্বসম বলা হয়। আর যদি দুটি ত্রিভুজ সর্বসম হয়, তাহলে ঐ ত্রিভুজ দুটির অনুরূপ বাহুগুলো ও অনুরূপ কোণগুলো পরস্পর সমান হয়ে যায়। |
এখন যদি ∆ABC ও △DEF পরস্পর সর্বসম হয়, তহলে আমরা ∆ABC = ∆DEF এভাবে লিখে প্রকাশ করি। এর অর্থ হলো ∆ABC ও △DEF পরস্পর সর্বসম।
এবার ত্রিভুজের সর্বসমতা প্রমাণের জন্য কী তথ্য প্রয়োজন? এ জন্য দলগতভাবে নিচের কাজটি কর:
| কাজ: ১. ∆ABC ও ∆DEF দুটি ত্রিভুজ আঁক, যাদের AB = DE = 5 সেমি, BC = EF = 6 সেমি এবং ∠ABC = ∠DEF = 60°1 ২. ত্রিভুজ দুটির তৃতীয় বাহুর দৈর্ঘ্য এবং অন্য কোণ দুটি পরিমাপ কর। ৩. তোমাদের পরিমাপগুলো তুলনা কর। এখান থেকে কি কিছু দেখতে পাচ্ছ? |
common.read_more